Základní úlohou kartografie je jednoznačné a přesné udání polohy objektu na zemském povrchu a jeho vyjádření v mapě. Protože mapa umožňuje zakreslit pouze rovinný obraz, je nutné polohu bodu na zemském povrchu vhodným způsobem promítnout do roviny mapy. Složitě členitý zemský povrch se postupně nahrazuje topografickou plochou, nulovou hladinovou plochou (geoidem) a následně referenční plochou (dvojosým rotačním elipsoidem, koulí, rovinou).
Na elipsoidu lze jednoznačně určit polohu pomocí zeměpisné šířky φ (řecké písmeno fí, latitude, Lat) a zeměpisné délky λ (lambda, longitude, Long). Těmto souřadnicím se říká zeměpisné nebo geografické a souřadnicový systém se nazývá geografický. Zeměpisné souřadnice bodů se určují astronomickým měřením. Hodnoty se měří a uvádí ve stupních (°), minutách (') a vteřinách ("). Platí že 1° = 60' a 1' = 60", pro lepší zapamatování to lze přirovnat k hodině, minutám a vteřinám.
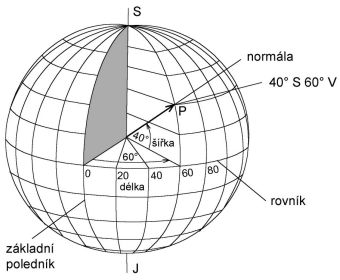
Rovina vedená kolmo k ose rotace středem Země vytne na matematickém povrchu Země kružnici zvanou rovník.Všechny roviny vedené rovnoběžně s rovníkem vytínají na matematickém povrchu Země kružnice nazývané rovnoběžky. Všechny roviny procházející osou rotace vytínají na matematickém povrchu Země poledníky (na elipsoidu budou mít tvar elipsy, na kouli kružnice). Základní poledník je dohodou přijatý poledník procházející významnou hvězdárnou. Na našich mapách se nejčastěji jako základní (nultý) poledník používá poledník procházející věží hvězdárny v Greenwichi u Londýna, občas se ještě setkáme s poledníkem Ferrským (dnes ho najdeme pod názvem Hierro v souostroví Kanárských ostrovů) , ležícím 17° 40´ západně od poledníku londýnské hvězdárny.
Zeměpisná šířka φ bodu je úhel v rovině poledníku mezi normálou bodu (jeho tížnicí) a rovinou rovníku. Počítá se ve stupních, a to od rovníku směrem na sever jako severní z.š. (0° - 90° s kladným znaménkem), od rovníku směrem na jih jako jižní z.š. (0° - 90° se záporným znaménkem). Zeměpisná délka λ bodu je úhel, který svírá poledníková rovina bodu s rovinou základního poledníku. Uvádí se ve stupních, a to od základního poledníku směrem na východ jako východní z.d. (0° - 180° s kladným znaménkem), od základního poledníku směrem na západ jako západní z.d. (0° - 180° se záporným znaménkem).
Chceme-li získat obraz bodu v rovině mapy, musíme promítnout referenční elipsoid na povrch vhodného tělesa (kužel, válec, rovina), který lze rozvinout do roviny. Po rozvinutí můžeme na této rovinné ploše definovat pravoúhlý (kartézský) souřadnicový systém, kde jednotkami budou zpravidla metry. Tento matematický postup (transformace zeměpisných souřadnic na pravoúhlé rovinné souřadnice) se nazývá kartografické zobrazení neboli projekce.
Zemský elipsoid má velmi malé zploštění (1:300), a tak jej v řadě případů můžeme nahradit koulí. A nakonec jedna velmi důležitá skutečnost: Pro nepříliš rozsáhlá území (do 700 km2) můžeme nahradit geoid rovinou.
To znamená, že při tvorbě map pro OB nemusíme uvažovat zkreslení daná zakřivením zemského povrchu. Mapa se tak konstruuje jako zmenšený rovinný obraz reliéfu a objektů na jeho povrchu zakreslených svými kolmými průměty.
Je na místě si rovněž definovat pojem mapa, přestože intuitivně víme, co si pod tímto pojmem máme představit. Mapou rozumíme zmenšené, zevšeobecněné zobrazení povrchu Země, ostatních nebeských těles nebo nebeské sféry, sestrojené podle matematického zákona na rovině a vyjadřující pomocí smluvených znaků rozmístění a vlastnosti objektů vázaných na jmenované povrchy.
Nutnost zmenšení mapy oproti skutečnosti je dostatečně zřejmá - důležité však je, že tento koeficient zmenšení(tedy poměr odpovídajících si vzdáleností na mapě a ve skutečnosti) nazýváme měřítko mapy. Obsah mapy vzhledem k použitému měřítku musí být oproti realitě zjednodušen neboli generalizován, aby byla zachována čitelnost mapy. V mapě tedy nebude zachyceno tolik objektů, které bychom našli např. na leteckém snímku shodného měřítka, který je však pouhou zmenšeninou skutečnosti. Matematickým zákonem je míněno kartografické zobrazení referenční plochy Země, ostatních nebeských těles nebo nebeské sféry na rovinu mapy. Smluvenými znaky jsou myšleny kartografické vyjadřovací prostředky (např. mapové značky, diagramy a další), z nichž se mapový obraz skládá. Pasáž rozmístění a vlastnosti objektů v definici nevystihuje beze zbytku reálnou skutečnost, neboť v mapách jsou vyjadřovány nejen objekty(budovy, komunikace, horstva atd.), ale také přírodní a společenské jevy (geofyzikální, klimatické, hospodářské, demografické atd.).
Mapy nejsou jediným kartografickým vyjádřením prostorově uspořádané skutečnosti. Bývají rovněž používány glóby s vyjádřením sférickým nebo plastické či reliéfní mapy s vyjádřením prostorovým.
Přesně znázornit povrch koule či elipsoidu do roviny není možné. Každé kartografické zobrazení vždy provází zkreslení geometrických prvků obrazu - úhlů, délek a plošných obsahů. Je to však způsob, jak zemské tvary znázornit v mapě s minimem takových nepřesností. Je známa celá řada rozdílných typů projekcí a jejich volba vždy závisí na účelu mapy. Má-li mapa zobrazit poměrně malé území zemského povrchu (např. území naší republiky), pak musí vybrané zobrazení velmi přesně znázorňovat vzdálenosti, úhly a tvary. V takovém případě se volí konformní zobrazení, které nezkresluje úhly. Má-li však mapa ukazovat rozsah obdělávané půdy na celém světě, pak je třeba zvolit zobrazení plochojevné neboli ekvivalentní, které zachová poměry plošných velikostí. Konformní projekce se až na výjimky nepoužívají pro mapy světa, protože polární oblasti neúměrně zveličují. Nejznámější příklad takového zobrazení, Mercatorova projekce, je však neocenitelným pomocníkem pro mořeplavce, neboť plavba pod stálým kursem bude v mapě zaznamenána jako přímka.
Existuje široká škála kartografických zobrazení, která lze zjednodušeně rozčlenit podle tří kritérií:
Některé projekce jsou čistě geometrické a lze je považovat za průměty rovnoběžek a poledníků z průhledného glóbu na přimknutý válec, kužel nebo rovinu.
Ostatní projekce jsou sestrojeny matematicky a obraz bodu v těchto projekcích nelze získat geometrickou cestou, ale výhradně numerickým přepočtením souřadnic bodu podle složitých matematických vztahů.
Pro zobrazení bodů na zemském povrchu se využívá referenčních ploch, které nahrazují nepravidelný geoid. Nejbližším tělesem je dvojosý rotační elipsoid s vhodně zvolenými rozměry, který rotuje kolem své vedlejší osy. Je charakterizován hlavní poloosou a (ze středu Země k rovníku), vedlejší poloosou b (ze středu k pólu) a zploštěním i = (a-b)/a. Rozměry elipsoidu se nejdříve určovaly ze stupňových měření provedených geodetickými metodami, později k tomu přistoupila astronomická a gravimetrická měření a dnes jsou to pozorování umělých družic Země. S rostoucím počtem pozorování a zvyšovanou přesností měření byla určena celá řada elipsoidů, která zpravidla nesou název po svém autorovi. Mezi nejvýznamnější z hlediska použití pro účely referenčních ploch jsou uvedeny v následující tabulce:
Parametry nejčastěji užívaných elipsoidů
| Název | Rok | Hlavní poloosa a | Vedlejší poloosa b | Zploštění i |
|---|---|---|---|---|
| Bessel | 1841 | 6377397,155 m | 6356078,963 m | 1:299,2 |
| Hayford | 1910 | 6378388,000 m | 6356911,946 m | 1:297 |
| Krasovskij | 1940 | 6378245,000 m | 6356863,019 m | 1:298,3 |
| WGS-84 | 1984 | 6378137,000 m | 6356752,314 m | 1:298,3 |
Pro mnohé účely geodézie a kartografie se nahrazuje elipsoid jednodušší referenční plochou kulovou, která je určena poloměrem. Toto zjednodušení usnadní výpočty a používá se zejména pro mapy světa. Poloměr referenční koule se volí tak, aby měla stejný objem jako referenční elipsoid. V určitých specifických případech se volí za referenční plochu přímo rovina - např. při azimutálním zobrazení. Pro zobrazení území o ploše menší než cca 700 km2 je rozdíl mezi elipsoidem a jeho tečnou rovinou tak zanedbatelný, že veškerá měření můžeme provádět v rovině.
Výběr a specifikace referenčního elipsoidu pro určitá území a jeho přesná orientace se označuje jako datum. V Evropě je nejčastěji používán elipsoid Besselův , Rusko a státy bývalého soc. bloku hojně užívají Krasovského elipsoid a v Americe je to Hayfordův elipsoid. Elipsoid WGS-84 je používán celosvětově v rámci globálního souřadnicového systému WGS.